Thread: Calculating the Bevel Angle

Just finished taking Calc I and was thinking about some trig principles today while showering and getting ready to shave. I thougth about honing and realized I could figure out the actual bevel angle put on a razor using trig. It's a pretty simple calculation if you're familiar with trig, here is how it works.

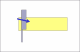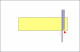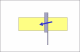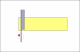
A straight razor laying flat against a hone establishes a right triangle, with a points of contact with the hone at the edge and the spine. By taking the spine width and dividing it by two, you get an approximate length of the opposite side of the triangle (side standing up), while the blade width provides the length of the hypotenuse (long side of triangle). By using the sin theta you don't need to calculate the bottom of the triangle as sin theta = opposite / hypotenuse. This allows us to get the actual angle between the hypotenuse and the adjacent side or bottom of the triangle (hone would be the adjacent side). I divided the spine width by two in order to get the angle from the exact center of the blade, where the very tip of the edge will be after honing. The angle would be exactly what would be established for the bevel after honing. By taking the arcsin of the fraction you get the angle because the formula reads...

sin theta = (opposite / hypotenuse)

Therefore...

arcsin(opposite / hypotenuse) = theta

theta = angle

Running some basic numbers you get the following bevel angles...

Spine Width......Blade Length.....Bevel Angle
3/16"..............5/8"................8.63 degrees
1/4"...............5/8"................11.54 degrees
3/16"..............3/4"................7.2 degrees
1/4"................3/4"...............9.6 degrees
3/16"...............7/8"..............6.2 degrees
1/4"...............7/8"................8.2 degrees
3/16"...............1".................5.4 degrees
1/4"...............1"..................7.2 degrees

Some generalizations can be made from the information gathered here...

As the spine gets thicker the bevel angle increases.

As the blade gets longer the bevel angle decreases.

A smiling edge will have a bevel angle that varies, being largest at the shortest part of the blade and smallest at the longest part of the blade. Between these points the bevel angle will vary from a greater angle to smaller angle and back to a greater angle, analyzing the blade from toe to heel or vice versa.

As an example, a smiling blade with 5/8" toe, 3/4" center and 5/8" heel with 3/16" spine will have a bevel angle varying from approximately 8.63 degrees at the toe to 7.2 degrees at the center and back to 8.63 degrees at the heel.

Wedges work a bit different if the entire blade rests against the hone while honing. If that is the case then the triangle's opposite side (standing up side) would go the entire length of the spine. If the blade does not rest against the hone and points of contact are only the spine and edge then the previous calculations using 1/2 the spine width work.

Just thought I'd throw this out there

Those angles need to be multiplied by 2 to get the full bevel angles.

Bad drawings, should've put spine against bottom line (hone) but this is why I divided by 2 hope you get idea.

Actually see your point now though if the bevel angle is calculated using the angle from both sides of the edge instead of just one.

I may be wrong but think the formula should be

tan theta = (opposite / adjacent)

You are using the Hypot. as the width but the width is from the back of the spine to the edge of the blade.


But they come out right which makes me believe we have been had! Probably an inverse function of arctan is sine. It has been to long since I have had it.

Take Care,
Richard

Originally Posted by riooso

I may be wrong but think the formula should be

tan theta = (opposite / adjacent)

But they come out right which makes me believe we have been had! Probably an inverse function of arctan is sine. It has been to long since I have had it.

Take Care,
Richard

I always remebered tangent as rise over run like slope. That would be opposite / adjacent which is right, if you calculated the adjacent side which would be the length of the bottom of the triangle that would work as well. You could use pythagorem to get the bottom of the triangle, but I used sine because the values were already known with less math for it.

Some interesting info here.

Regards,
Neil

That's interesting that 18 degrees is the ideal angle, maybe that is why some razors shave better than others not only does the quality of steel matter but also the geometry with which the blade was made, as that ultimately determines the bevel angle when honing, unless the spine is taped which alters the angle. Looking at those pictures I noticed something else as well. Depending on how the razor lays on the hone can change the hypotenuse (long side/blade) of the triangle by making it slightly shorter. Most spines are rounded or something similar so the blade rests on the hone with a point of contact slightly less than the entire length of the blade which will give a slightly steeper angle than if you used the entire blade length in calculation.

Another lame drawing to illustrate

So now I'm curious do our custom razor manufacturers use such information to determine the angle of bevel that will ultimately end up on the custom razor that they're creating?

The traditional calc is blade width divided by spine thickness. Some of the old articles I have read say it should be a 3.5:1 ratio.
My goal is 3.5:1 ratio blade width/spine thickness. I like the greater angle since it results in a smaller bevel width which makes it easier to hone.



3/16"..............5/8"................8.63 degrees...... ratio 3.33
1/4"...............5/8"................11.54 degrees .....ratio 2.5
3/16"..............3/4"................7.2 degrees ........ratio 4.0
1/4"................3/4"...............9.6 degrees .........ratio 3.0
3/16"...............7/8"..............6.2 degrees .........ratio 4.6
1/4"...............7/8"................8.2 degrees .........ratio 3.5
3/16"...............1".................5.4 degrees .........ratio 5.3
1/4"...............1"..................7.2 degrees ..........ratio 4.0

Just my $.02,

Originally Posted by randydance062449

The traditional calc is blade width divided by spine thickness. Some of the old articles I have read say it should be a 3.5:1 ratio.
My goal is 3.5:1 ratio blade width/spine thickness. I like the greater angle since it results in a smaller bevel width which makes it easier to hone.



3/16"..............5/8"................8.63 degrees...... ratio 3.33
1/4"...............5/8"................11.54 degrees .....ratio 2.5
3/16"..............3/4"................7.2 degrees ........ratio 4.0
1/4"................3/4"...............9.6 degrees .........ratio 3.0
3/16"...............7/8"..............6.2 degrees .........ratio 4.6
1/4"...............7/8"................8.2 degrees .........ratio 3.5
3/16"...............1".................5.4 degrees .........ratio 5.3
1/4"...............1"..................7.2 degrees ..........ratio 4.0

Just my $.02,

I see, the numbers I used to calc were all just hypothetical to get an idea of the effect of varying the blade width and spine thickness. If you multiplied the angles by 2 to get the full angle of the edge it looks as though it is about 16 degrees at a ratio of 3.5:1.

If you are interested in this topic, you might enjoy reading thru this thread: http://straightrazorpalace.com/advan...ed-taping.html