Thread: Computing the angle...

Oh, do I ever know that it will turn out fine! Just as long as I don't develop carpal tunnel syndrome first! The question came to mind because of some of the extremely bad straight razors that I have seen. Some how, some way,
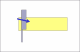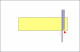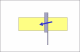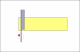
people have managed to make the width of the blade at the toe narrower without proportionatly decreasing the thickness of the spine. The result is that the razor will not lay flat on the hone. Trying to figure out how much the spine thickness needed to be reduced was the motivationfor the question.

Originally Posted by aschaab

for your question a general purpose formula would be angle=asin(Spine/Blade), so in your case angle=asin(1/8" / 5/8")=11.5°. Comment: asin is the inverted sine Function

This is not correct. The correct formula is:
angle = 2arctan (.5spine/blade)

Your formula is approximately correct because the bevel angle is so small. If the angle was larger, it would be wrong.

Here's why. You need to visualize the razor being honed. The bevel angle is the angle between the hone and the plane of the blade, which form two sides of a triangle. The third side is half the spine. The TAN of that angle is .5spine/blad. So, the bevel angle is arctan (.5spine/blade). The blade angle is twice the bevel angle.

With our numbers, the angle is actually 11.4 degrees. As I said above, the error would be much larger with larger angles.

Originally Posted by 440stainless

I think theres a slight problem with the algebra there. Trigonometric functions work only for right triangles. The only right triangle you can really make there is by laying the blade on a flat surface. The hypotenuse of the right triangle is the line from the very edge of the blade to the middle of the spine (when looking at it end-on) and tue only leg of the triangle that you can measure is the line from the tip of the blade to the point at which the spine touches the hone.

The two lengths you know form the angle you want to find out (or rather half of the angle). So you use the inverse cosine function: acos(leg/hypotenuse) and multiply that angle by two to get the full angle of the blade. If you want a formula for the width of the spine at a given point on the blade, you can extrapolate a linear function for the width of the blade at a given point and use it to create a function that gives the width of the spine.

You don't know the hypotenuse. You only know the opposite side (half the spine) and the adjacent side (the width of the blade). So, you're really dealing with a tangent.

Originally Posted by randydance062449

Thanks for the reply.

I would venture a guess that the previous example's answer of 11.5 degrees
is close to the full "included" angle and that if we divide that by 2 we will be close to the actual angle. But thats only a guess on my part. I will look and see what is posted on the other forums. This should be interesting.

The error in the answer is small because it's a small angle, but the formula is wrong.

Originally Posted by randydance062449

Oh, do I ever know that it will turn out fine! Just as long as I don't develop carpal tunnel syndrome first! The question came to mind because of some of the extremely bad straight razors that I have seen. Some how, some way,
people have managed to make the width of the blade at the toe narrower without proportionatly decreasing the thickness of the spine. The result is that the razor will not lay flat on the hone. Trying to figure out how much the spine thickness needed to be reduced was the motivationfor the question.

I have a few of those. The two seems to curve up radically, with a much steeper bevel at the toe than the rest of the blade. It seems to work OK. I just don't like the way it looks.

I hone it by using a sweeping motion rather than trying to lie the razor flat.

Originally Posted by Joe Lerch

This is not correct. The correct formula is:
angle = 2arctan (.5spine/blade)

Hi Joe,

yes, I stand corrected - it always helps to spend a few more minutes on thinking about things like this

Thanks for pointing this out,
-Axel-