Thread: Computing the angle...

Ok guys, here are two question's for you.

1.What is the formula to compute the angle for our straight razors.
Give me an example please.

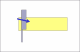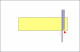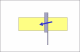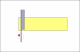
Lets assume that the blade width is 5/8ths and the thickness of the spine
is 1/8th.

2. Another question. lets say we just purchased an Ebay special. The prior owner for some reason has made a gradual taper to the width of the blade going from the heel at its widest, 5/8ths, to the toe of the blade, 4/8ths. Let assume he ground it down to remove some big nicks in the blade and he used an electric kitchen knife sharpener so the spine was not touched. Now the thickness of the spine is 1/8th.
Since we know that the ratio of the blade width divided by the thickness of the spine determines the angle and we know that the ratio must be constant for the entire length of the blade in order for the blade to lay flat on the hone, then, what thickness must the spine be at the toe of the blade in order to compensate for the decrease in the blade width?

5/8 divided by 1/8 = 5
4/8 divided by ? = 5
or .5/?=5
?=0.1 or 1/10th of an inch?

What would be a general purpose formula to solve this?

Sorry, my algebra is failing me,

Hi Randy,

ad 1): its basic geometry , so for your question a general purpose formula would be angle=asin(Spine/Blade), so in your case angle=asin(1/8" / 5/8")=11.5°. Comment: asin is the inverted sine Function

ad 2): the same formula applies for your problem, and in fact you already solved it You just calculate your angle in one part of the blade, lets call it "angle1". Now you go to the other part of the blade and play a bit with the formula to turn out Spine1=sin(angle1)*Blade1. As shown in ad 1) angle1 in your case is 11.5° and sin(11.5°)=0.2 so this leads to Spine1=0.2*4/8"=0.1".

Hope I did not confuse you too much ,
-Axel-

Thanks guy!

Now, to get to the meat of the problem.

I do not have a calculator capable of computing the asin or sin function.

What formula can I use to work this out on paper.
asin = ?
sin = ?

Originally Posted by aschaab

for your question a general purpose formula would be angle=asin(Spine/Blade), so in your case angle=asin(1/8" / 5/8")=11.5°. Comment: asin is the inverted sine Function

This is not correct. The correct formula is:
angle = 2arctan (.5spine/blade)

Your formula is approximately correct because the bevel angle is so small. If the angle was larger, it would be wrong.

Here's why. You need to visualize the razor being honed. The bevel angle is the angle between the hone and the plane of the blade, which form two sides of a triangle. The third side is half the spine. The TAN of that angle is .5spine/blad. So, the bevel angle is arctan (.5spine/blade). The blade angle is twice the bevel angle.

With our numbers, the angle is actually 11.4 degrees. As I said above, the error would be much larger with larger angles.

Originally Posted by Joe Lerch

This is not correct. The correct formula is:
angle = 2arctan (.5spine/blade)

Hi Joe,

yes, I stand corrected - it always helps to spend a few more minutes on thinking about things like this

Thanks for pointing this out,
-Axel-

use the windows OS calc applet and change to scientific functions.

Start > Run > "calc" > View > Scientific

That should get your all the geometric functions you need.

Thanks guys!

I now have what I was looking for, either a formula or a constant for asin and sin. Now I have them

asin= 57.68479516........
sin= .017391304..........

so

angle of blade= asin(thickness of spine/ width of blade)
57.68479516(1/8 divided by 5/8)
57.68479516(.125/.625)
57.68479516(.2)= 11.5......

To compute the desired thickness of the spine at a specific spot on the blade so that the angle of the blade is constant when the width of the blade is not constant the formula is

Desired spine thickness at point2 =sin(angle of blade at point 1)*(blade width at point 2.)

.017391304(11.5)*0.5= 0.0999999 or .1 or 1/10th of an inch.

Thanks Axel!

must be voodoo 'r some devil speak maybe.

I think theres a slight problem with the algebra there. Trigonometric functions work only for right triangles. The only right triangle you can really make there is by laying the blade on a flat surface. The hypotenuse of the right triangle is the line from the very edge of the blade to the middle of the spine (when looking at it end-on) and tue only leg of the triangle that you can measure is the line from the tip of the blade to the point at which the spine touches the hone.

The two lengths you know form the angle you want to find out (or rather half of the angle). So you use the inverse cosine function: acos(leg/hypotenuse) and multiply that angle by two to get the full angle of the blade. If you want a formula for the width of the spine at a given point on the blade, you can extrapolate a linear function for the width of the blade at a given point and use it to create a function that gives the width of the spine.

Thanks for the reply.

I would venture a guess that the previous example's answer of 11.5 degrees
is close to the full "included" angle and that if we divide that by 2 we will be close to the actual angle. But thats only a guess on my part. I will look and see what is posted on the other forums. This should be interesting.

Originally Posted by 440stainless

I think theres a slight problem with the algebra there. Trigonometric functions work only for right triangles. The only right triangle you can really make there is by laying the blade on a flat surface. The hypotenuse of the right triangle is the line from the very edge of the blade to the middle of the spine (when looking at it end-on) and tue only leg of the triangle that you can measure is the line from the tip of the blade to the point at which the spine touches the hone.

The two lengths you know form the angle you want to find out (or rather half of the angle). So you use the inverse cosine function: acos(leg/hypotenuse) and multiply that angle by two to get the full angle of the blade. If you want a formula for the width of the spine at a given point on the blade, you can extrapolate a linear function for the width of the blade at a given point and use it to create a function that gives the width of the spine.