Thread: Computing the angle...

Ok guys, here are two question's for you.

1.What is the formula to compute the angle for our straight razors.
Give me an example please.

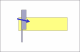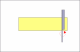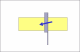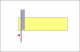
Lets assume that the blade width is 5/8ths and the thickness of the spine
is 1/8th.

2. Another question. lets say we just purchased an Ebay special. The prior owner for some reason has made a gradual taper to the width of the blade going from the heel at its widest, 5/8ths, to the toe of the blade, 4/8ths. Let assume he ground it down to remove some big nicks in the blade and he used an electric kitchen knife sharpener so the spine was not touched. Now the thickness of the spine is 1/8th.
Since we know that the ratio of the blade width divided by the thickness of the spine determines the angle and we know that the ratio must be constant for the entire length of the blade in order for the blade to lay flat on the hone, then, what thickness must the spine be at the toe of the blade in order to compensate for the decrease in the blade width?

5/8 divided by 1/8 = 5
4/8 divided by ? = 5
or .5/?=5
?=0.1 or 1/10th of an inch?

What would be a general purpose formula to solve this?

Sorry, my algebra is failing me,

Hi Randy,

ad 1): its basic geometry , so for your question a general purpose formula would be angle=asin(Spine/Blade), so in your case angle=asin(1/8" / 5/8")=11.5°. Comment: asin is the inverted sine Function

ad 2): the same formula applies for your problem, and in fact you already solved it You just calculate your angle in one part of the blade, lets call it "angle1". Now you go to the other part of the blade and play a bit with the formula to turn out Spine1=sin(angle1)*Blade1. As shown in ad 1) angle1 in your case is 11.5° and sin(11.5°)=0.2 so this leads to Spine1=0.2*4/8"=0.1".

Hope I did not confuse you too much ,
-Axel-

Thanks guy!

Now, to get to the meat of the problem.

I do not have a calculator capable of computing the asin or sin function.

What formula can I use to work this out on paper.
asin = ?
sin = ?

use the windows OS calc applet and change to scientific functions.

Start > Run > "calc" > View > Scientific

That should get your all the geometric functions you need.

Thanks guys!

I now have what I was looking for, either a formula or a constant for asin and sin. Now I have them

asin= 57.68479516........
sin= .017391304..........

so

angle of blade= asin(thickness of spine/ width of blade)
57.68479516(1/8 divided by 5/8)
57.68479516(.125/.625)
57.68479516(.2)= 11.5......

To compute the desired thickness of the spine at a specific spot on the blade so that the angle of the blade is constant when the width of the blade is not constant the formula is

Desired spine thickness at point2 =sin(angle of blade at point 1)*(blade width at point 2.)

.017391304(11.5)*0.5= 0.0999999 or .1 or 1/10th of an inch.

Thanks Axel!

must be voodoo 'r some devil speak maybe.

I think theres a slight problem with the algebra there. Trigonometric functions work only for right triangles. The only right triangle you can really make there is by laying the blade on a flat surface. The hypotenuse of the right triangle is the line from the very edge of the blade to the middle of the spine (when looking at it end-on) and tue only leg of the triangle that you can measure is the line from the tip of the blade to the point at which the spine touches the hone.

The two lengths you know form the angle you want to find out (or rather half of the angle). So you use the inverse cosine function: acos(leg/hypotenuse) and multiply that angle by two to get the full angle of the blade. If you want a formula for the width of the spine at a given point on the blade, you can extrapolate a linear function for the width of the blade at a given point and use it to create a function that gives the width of the spine.

Thanks for the reply.

I would venture a guess that the previous example's answer of 11.5 degrees
is close to the full "included" angle and that if we divide that by 2 we will be close to the actual angle. But thats only a guess on my part. I will look and see what is posted on the other forums. This should be interesting.

Originally Posted by 440stainless

I think theres a slight problem with the algebra there. Trigonometric functions work only for right triangles. The only right triangle you can really make there is by laying the blade on a flat surface. The hypotenuse of the right triangle is the line from the very edge of the blade to the middle of the spine (when looking at it end-on) and tue only leg of the triangle that you can measure is the line from the tip of the blade to the point at which the spine touches the hone.

The two lengths you know form the angle you want to find out (or rather half of the angle). So you use the inverse cosine function: acos(leg/hypotenuse) and multiply that angle by two to get the full angle of the blade. If you want a formula for the width of the spine at a given point on the blade, you can extrapolate a linear function for the width of the blade at a given point and use it to create a function that gives the width of the spine.

Randy, just hone the dam razor...

Hehe. He may have a point Randy. When you're doing any sort of weird inverse trigonometric function to get an angle, the answer you get is only as exact as the measurements you take. In the case of this razor (and razors in general) you're dealing with fairly small distances which you might have better luck measuring with calipers or something and it feels like one would mess up the edge with one of those. You can probably just do it by feel and it'll turn out fine.